

Every time the algorithm moves through the list, it’s known as a ‘pass.’įor sorting an array in ascending order, the first iteration moves the largest value to the last position of the array. This process of comparing and interchanging repeated until the largest element bubbled from its original position to the correct place in the final sorted array. second and third elements are compared and swapped if necessary and so on). We then move to the next higher position element and repeat this process (i.e. first and second elements compared and swapped if first is greater than the second). In Bubble Sort, the first pass starts by comparing the adjacent pair of elements in the array starting at one end and swap (interchange) them if they are not in the proper order (i.e. The bubble sort algorithm has the same efficiency as the selection sort algorithm. Bubble sort is not difficult to implement, and it’s fast enough once you have small data sets. For this, it uses several passes through the array and in each pass, the largest element searches its proper position in the sorted array. It requires (n-1) passes to sort an array. Now for every index i, we run an inner loop from j = i to n - 1 and find the index of the minimum value in the unsorted part.Bubble sort in C is the most straightforward sorting algorithm called a sinking sort, and It works by repeatedly moving the largest elements to the highest index position in the array (if elements are to arranged in ascending order).

In general, at the ith step of the algorithm, it maintains two subarrays:
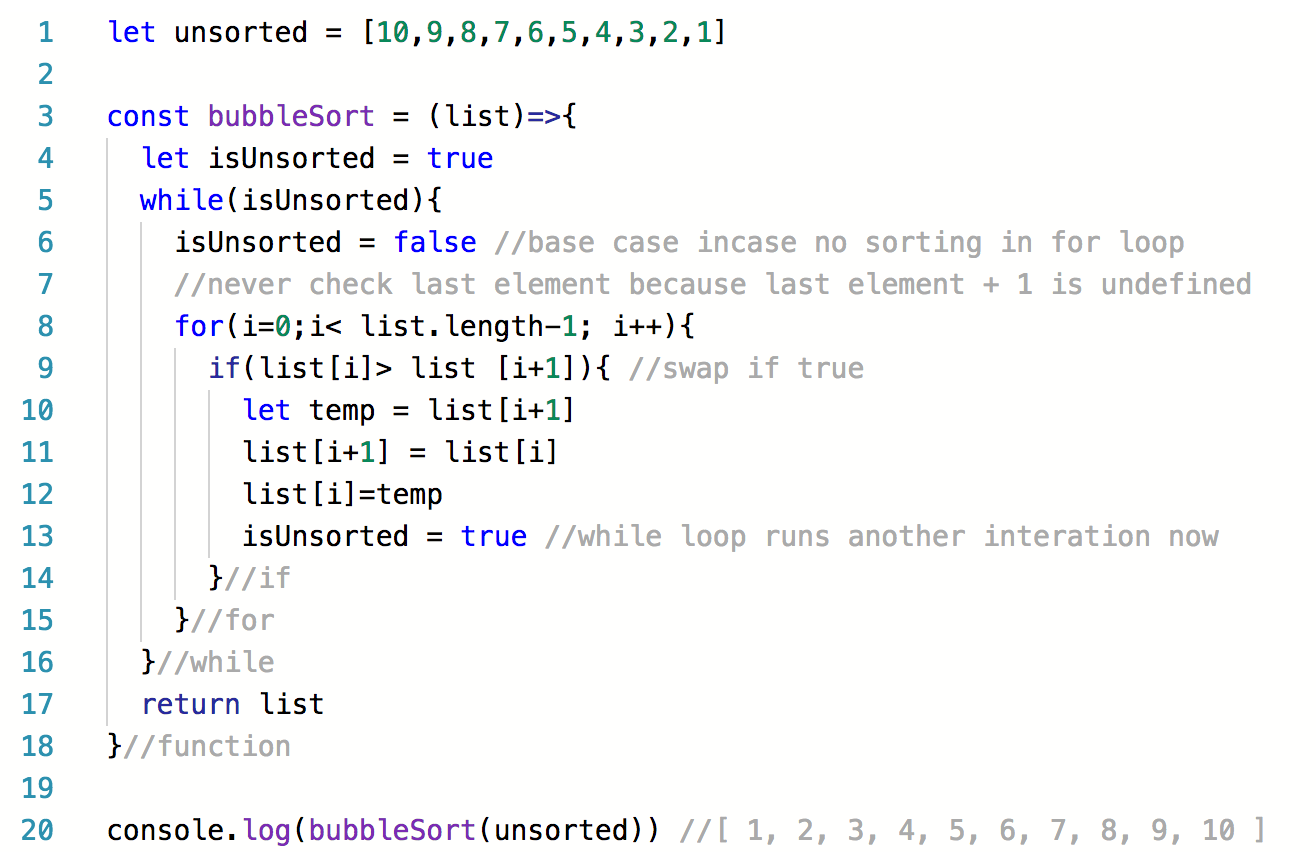
This process goes on till the whole array gets sorted.

Then we again look for the smallest element in the remaining array (excluding the first element) and swap it with the second element. Once we find it, we swap the smallest element with the first element of the array. The idea of the selection algorithm is simple: we traverse the whole array to find the smallest element. How can we sort linked lists and strings using bubble sort algorithm?.Can we think to implement the bubble sort recursively?.Can we modify the above pseudo-code to sort elements in decreasing order?.What is the idea of "stability" in the case of sorting algorithms? is bubble sort a stable sorting algorithm?.What would be the average case time complexity of the bubble sort?.But there is no improvement in worst-case time complexity which is still O(n^2) for the reverse sorted array. So, O(n) is the best-case running time for the bubble sort. In the above implementation, if an array is already sorted, then bubble sort makes no swaps, and the algorithm can terminate after a single pass. So we need to run an inner loop from n - i - 1 time. At (i + 1)th iteration of the outer loop, we place (i + 1)th maximum element at (n - i -1)th index. So outer loop will run n times from i = 0 to n - 1.Īfter the first ith iteration of the outer loop, i maximum elements will get placed from an index (n - i) to (n - 1). At each stage of the outer loop, we place one input value to its correct position in the sorted output.This process will go on till the whole array becomes sorted. In general, at any ith iteration, we place the ith maximum element at (n - i)th index.Similarly, after the 2nd iteration, the 2nd largest element in the array bubbles up towards the (n - 2)th index. After the end of 1st iteration, the largest element in the array bubbles up towards the (n - 1)th index.Now again traverse the array from 0 to n - 2 and place the second largest element at the (n - 2)th index and.so on. So one basic idea would be to traverse the array from 0 to n - 1 and place the largest element at the (n - 1)th index. If we look at the element in the sorted array: the largest element is at the (n - 1)th index, 2nd largest is at (n - 2)th index, and so on. Sometimes It is also referred to as a "Sinking Sort"! It is generally one of the basic algorithms taught in programming to develop an intuition about the working of algorithms. <= X <= X Bubble Sort Algorithmīubble sort is a simple and inefficient sorting algorithm. Output: A permutation of input such that X <= X <= X.


 0 kommentar(er)
0 kommentar(er)
